Définition de théorème
Tirant son origine du latin theorēma, le mot théorème consiste en une proposition pouvant être démontrée de manière logique à partir d’un axiome ou d’autres théorèmes ayant été préalablement démontrés. Ce processus de démonstration a lieu au moyen de certaines règles d’inférence.
Le théorème peut être décrit comme une affirmation d’importance. Il existe certaines affirmations de rang plus bas, comme c’est le cas du lemme (proposition appartenant à un théorème plus grand, soit celle qui prépare la démonstration d’une autre), le corolaire (proposition suivant immédiatement le théorème, soit une conséquence découlant d’une proposition venant d’être démontrée) ou la proposition (un résultat n’étant associé à aucun théorème en particulier).
Tant que l’affirmation n’est pas démontrée, on parle alors d’hypothèse ou de conjecture.
Parmi les théorèmes les plus populaires, il y a lieu de mentionner le Théorème de Thalès, d’après lequel, si l’on trace dans un triangle une ligne qui soit parallèle à l’un de ses côtés, on obtient deux triangles semblables (c’est-à-dire, deux figures ayant des angles identiques et des côtés proportionnels).
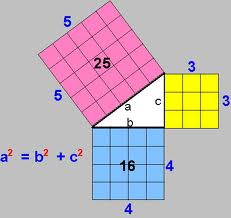
Par ailleurs, le Théorème de Pythagore défend que le carré de la longueur de l’hypoténuse (c’est-à-dire, le côté le plus long et qui s’oppose à l’angle droit) dans un triangle rectangle est égal à somme des carrés des longueurs des autres côtés (c’est-à-dire, les deux côtés les plus petits du triangle rectangle).




