Définition de demi-droite
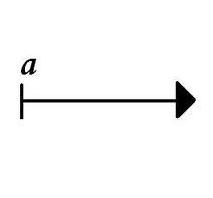
Demi-droite est un concept géométrique qui fait allusion à chacune des deux portions où la droite est divisée par n’importe lequel de ses points. Il est important de préciser que le terme correct est demi-droite (avec un tiret) et non pas demidroite.
Or, la demi-droite est la partie d’une droite qui est formée par tous les points qui se trouvent d’un côté d’un point fixe : cela veut dire qu’une demi-droite a un premier point (l’origine) mais il s’étend à l’infini. La droite, en revanche, n’a aucun point de départ ni de fin.
Autrement dit, la droite est une succession infinie de points. La demi-droite possède un point d’origine à partir duquel se suivent sans cesse des points. Le segment, à son tour, relève de l’intersection de l’ensemble des points de deux demi-droites (il y a un début et une fin).
La désignation demi-ligne fermée n’est pas d’autant plus fausse, étant donné que celle-ci inclue le point d’origine sauf qu’elle s’étend à l’infini, à l’image de la demi-droite.
Concernant la bijection entre une droite et les réels, on peut dire que les nombres réels positifs correspondent à l’une des demi-droites tandis que les nombres réels négatifs correspondent à l’autre. Le zéro, pour sa part, est le point frontière (origine) des deux demi-droites.
Pour comprendre ce qu’est une demi-droite, il suffit d’imaginer une règle qui commence par le chiffre 0 et qui s’étend dans un ordre naturel jusqu’à l’infini (0, 1, 2, 3, 4, 5, etc.).




